For all you physics gurus
Pages
- 1
- 2
| Author | Topic: For all you physics gurus |
|---|---|
|
Master
Member # 4614
|
written Wednesday, November 14 2007 16:17
Profile
Homepage
I'm having trouble understanding the coefficients of friction. For example, "The coefficient of kinetic friction between the block and the incline is 0.40. What is the magnitude of the acceleration of the suspended block as it falls? Disregard any pulley mass or friction." Image of the block and then incline:  Thanks for your help, even though I know you are all disappointed that I haven't been contributing much lately. :( [ Wednesday, November 14, 2007 16:18: Message edited by: Sturg ] -------------------- -ben4808 Posts: 3360 | Registered: Friday, June 25 2004 07:00 |
|
By Committee
Member # 4233
|
written Wednesday, November 14 2007 16:39
Profile
Hmm. It's been a LOOOOOOONG time for me on this, but wouldn't it be 1.6? -------------------- In today’s America, there are more World of Warcraft players than farmers. Posts: 2242 | Registered: Saturday, April 10 2004 07:00 |
|
...b10010b...
Member # 869
|
written Wednesday, November 14 2007 17:16
Profile
Homepage
You know what a normal force is, right? The frictional force is equal to the normal force multiplied by the coefficient of friction. -------------------- The Empire Always Loses: This Time For Sure! Posts: 9973 | Registered: Saturday, March 30 2002 08:00 |
|
Law Bringer
Member # 335
|
written Wednesday, November 14 2007 17:52
Profile
Homepage
I'll assume you've already worked on blocks on inclined planes and pulley systems. Friction just adds another force opposite the direction of motion equal to the coefficient of friction multiplied by the normal force, as Thuryl says. It's just one more term on your force diagram. —Alorael, who will work through all the numbers if it's necessary and if that isn't cheating. Posts: 14579 | Registered: Saturday, December 1 2001 08:00 |
|
Agent
Member # 2820
|
written Wednesday, November 14 2007 17:53
Profile
Ideally, I could draw diagrams for you, and it would make this much easier to explain. But I'll try my best. First, draw a free body diagram for the small block. The axis should be tilted counterclockwise 40 deg, so that the positive x-direction is parallel to the tension force T in the string. There should be four forces on the small block (I'm assuming you know which way these forces point): 1) normal force n, which prevents the block from falling through the floor 2) weight = mg 3) tension T 4) friction f = un where u = 0.4 = the coefficient of kinetic friction The acute angle between the weight vector (which points straight down) and the y-axis of the rotated coordinate system is 40 deg. This will be necessary to know later on. The sum of the forces in the y-direction should be 0 because the block does not accelerate into the floor. n - mg cos(40 deg) = 0 n = mg cos(40 deg) The cosine function comes from the triangle relationship you see on the FBD. The sum of the forces in the x-direction is ma, where a is a positive acceleration. T - f = ma T - un = ma T - mgu cos(40 deg) = ma T = mgu cos(40 deg) + ma Now draw a free body diagram for the bigger block. From here, it is a matter of personal taste regarding the labeling of the axis. Since the big block will accelerate downward when released, I will define the down direction as the positive x-direction so that the second block will have a positive acceleration a. Since the blocks are attached by a string, their accelerations should be same. There should be two forces, the same tension T from the first part and a weight 2mg. The following equation is the sum of the forces in the x-direction for the bigger block. Note that on the "ma" side of the F=ma equation that 2m is used since the bigger block has a mass of 2m. This is also why the weight is now 2mg. 2mg - T = 2ma 2mg - (mgu cos(40 deg) + ma) = 2ma 2mg - mgu cos(40 deg) - ma = 2ma 2mg - mgu cos(40 deg) = 3ma Cancelling out the m's yields 2g - gu cos(40 deg) = 3a a = (2g - gu cos(40 deg))/3 = 5.53 m/s^2 -------------------- Thuryl: I mean, most of us don't go around consuming our own bodily fluids, no matter how delicious they are. ==== Alorael: War and violence would end if we all had each other's babies! ==== Drakefyre: Those are hideous mangos. Posts: 1415 | Registered: Thursday, March 27 2003 08:00 |
|
Law Bringer
Member # 2984
|
written Wednesday, November 14 2007 18:04
Profile
Homepage
Well, since the pulley pulls in parallel to the slope, is the only normal force generated by the weight of mass M itself? (Sorry, it's been three years since I had physics...) In that case, the vertical vector of M's weight can be split up into a vector cos(40°)*M*g parallel to the slope (and down the slope, of course), as well as a vector sin(40°)*M*g orthogonal (normal) to the slope. The force of 2M's pulling on the pulley is (thanks to negligible pulley friction) equal to 2M*g. From this must be subtracted the vector cos(40°)*M*g, which pulls in the opposite direction. The frictional force is 0.4*sin(40°)*M*g, which is also subtracted. You end up with a force of (2-0.4sin(40°)-cos(40°)) *M*g, which acts on a mass M to produce an acceleration of (2-0.4sin(40°)-cos(40°))*g. I'm not sure if I calculated this correctly though, because it seems a bit strange that the acceleration would be independent of the value of M. -------------------- The Noble and Ancient Order of Polaris - We're Not Yet Dead. Encyclopedia • Blades Forge • Archives • Stats • RSS (This Topic / Forum) • Blog • NaNoWriMo Did-chat thentagoespyet jumund fori is jus, hat onlime gly nertan ne gethen Firyoubbit 'obio.' Decorum deserves a whole line of my signature, and an entry in your bookmarks. Posts: 8752 | Registered: Wednesday, May 14 2003 07:00 |
|
Off With Their Heads
Member # 4045
|
written Wednesday, November 14 2007 19:26
Profile
Homepage
Garrison is substantially correct, but he forgot that gravity also has a component in the x-direction. Aran is also substantially correct, but I'm not sure that he mentioned the factor of three that he needs in the answer. In any case, here's one way to get it. The proper axes for analyzing the block on the inclined plane are an axis parallel to the plane and an axis perpendicular. Perpendicular to the plane, the normal force balances the component of gravity: F_net = 0 n - Mg cosθ = 0 n = Mg cosθ Parallel to the plane, tension opposes friction and another component of gravity: F_net = Ma T - f - Mg sinθ = Ma T = f + Mg sinθ + Ma Since f = μn, and n was found above: T = μMg cosθ + Mg sinθ + Ma Now the hanging mass. I'll define up as positive, which means, since it's falling, its acceleration is in the negative direction. Use that the tension is equal to the tension found above. F_net = 2Ma T - 2mg = -2Ma μMg cosθ + Mg sinθ + Ma - 2Mg = -2Ma Cancel M's and move the a's to one side: μg cosθ + g sinθ - 2g = -2a - a Factor out the g: a = (g)(-1/3)(μ cosθ + sinθ - 2) Plugging in values, this yields a = 3.43 m/s^2. Note that my final expression is the same as Garrison's but for the gravity term parallel to the plane (the one with a sine in it). As for Aran's question, why the masses would cancel, that's what normally happens when we're solving for accelerations in fields of gravity in elementary physics! The acceleration due to gravity usually doesn't depend on mass. [ Wednesday, November 14, 2007 19:27: Message edited by: Kelandon ] -------------------- Arancaytar: Every time you ask people to compare TM and Kel, you endanger the poor, fluffy kittens. Smoo: Get ready to face the walls! Ephesos: In conclusion, yarr. Kelandon's Pink and Pretty Page!!: the authorized location for all things by me The Archive of all released BoE scenarios ever Posts: 7968 | Registered: Saturday, February 28 2004 08:00 |
|
Infiltrator
Member # 4256
|
written Wednesday, November 14 2007 19:46
Profile
Since that's nicely solved for you, I'd like to take advantage of the topic to ask a mechanics question too. It's showed up for me twice, and neither time have I taken the time to solve it correctly, but it bothers me. Put a brick of mass m and negligible size on top of a dome with a frictionless surface, made up of half a sphere of radius r (think slick igloo). Let the brick have an initial velocity of v in a horizontal direction. At what angle from the ground (in the plane of the bricks motion) will the brick no longer be in contact with the dome? -------------------- "Let's just say that if complete and utter chaos was lightning, he'd be the sort to stand on a hilltop in a thunderstorm wearing wet copper armour and shouting 'All gods are false'." Posts: 564 | Registered: Wednesday, April 14 2004 07:00 |
|
Law Bringer
Member # 2984
|
written Wednesday, November 14 2007 20:08
Profile
Homepage
Ouch. Indeed I forgot the factor 3, and it's a beginner error. I calculated the force exerted by the 2M mass, but forgot to factor in that this same force also has to act on the 2M mass itself. However, this makes my answer off by more than just a factor 3 - and I suspect I've made another mistake in there. -------------------- The Noble and Ancient Order of Polaris - We're Not Yet Dead. Encyclopedia • Blades Forge • Archives • Stats • RSS (This Topic / Forum) • Blog • NaNoWriMo Did-chat thentagoespyet jumund fori is jus, hat onlime gly nertan ne gethen Firyoubbit 'obio.' Decorum deserves a whole line of my signature, and an entry in your bookmarks. Posts: 8752 | Registered: Wednesday, May 14 2003 07:00 |
|
Master
Member # 4614
|
written Wednesday, November 14 2007 20:17
Profile
Homepage
Oof, it looks like UBB gnawed a little bit on some special HTML characters, Kel. I can still peice together what you were trying to say, though. Thanks much for everyone's responses. You were all extremely helpful, much more than I had expected. I'm in an online physics class currently, and problems like this are made a lot harder without an actual teacher to get help from when I have a problem. Super-smart whiz kids on Spiderweb do nicely, though. :cool: -------------------- -ben4808 Posts: 3360 | Registered: Friday, June 25 2004 07:00 |
|
Law Bringer
Member # 2984
|
written Wednesday, November 14 2007 21:05
Profile
Homepage
Oh, I saw my second error. The slope is 40° from the ground, hence it is 50° from the vertical vector. I saw it as 40° from the vertical because I read the diagram wrong. In practice, this either means I have to replace my value of theta s/40/50, or I have to exchange sine and cosine, which means the same thing. My earlier result was 3.19, now I get 3.436, which is closer to what Kel got. The difference may be in the value for g, which I estimated as 9.81. -------------------- The Noble and Ancient Order of Polaris - We're Not Yet Dead. Encyclopedia • Blades Forge • Archives • Stats • RSS (This Topic / Forum) • Blog • NaNoWriMo Did-chat thentagoespyet jumund fori is jus, hat onlime gly nertan ne gethen Firyoubbit 'obio.' Decorum deserves a whole line of my signature, and an entry in your bookmarks. Posts: 8752 | Registered: Wednesday, May 14 2003 07:00 |
|
Agent
Member # 2820
|
written Wednesday, November 14 2007 21:17
Profile
Jesus, I can't believe I messed that problem up. Things get lost accidentally pretty easily when you have no diagram to look at. -------------------- Thuryl: I mean, most of us don't go around consuming our own bodily fluids, no matter how delicious they are. ==== Alorael: War and violence would end if we all had each other's babies! ==== Drakefyre: Those are hideous mangos. Posts: 1415 | Registered: Thursday, March 27 2003 08:00 |
|
Agent
Member # 2820
|
written Wednesday, November 14 2007 21:30
Profile
OK, I definitely know how to solve Sticky's problem. Due to the nature of the problem, I'm going to assume that you are pretty familiar with the procedure I'm going to outline without all the equations. Draw a diagram where the block is still sliding down in contact with the igloo. Label the appropriate angles. Make a free body diagram at that point, with one of the axis pointing toward the center of the igloo. Make sure that you have the correct angle in your FBD for the weight force. You know that the sum of forces in the radial direction will be equal to mv^2/r. When the normal force is zero, the object is about to slip off. You should now have an equation with two unknowns: velocity and an angle. Now use conservation of energy to find out what v is in terms of the angle. You can do this because the object is on a spherical igloo, which allows you to use trigonometry. Then do the algebra. -------------------- Thuryl: I mean, most of us don't go around consuming our own bodily fluids, no matter how delicious they are. ==== Alorael: War and violence would end if we all had each other's babies! ==== Drakefyre: Those are hideous mangos. Posts: 1415 | Registered: Thursday, March 27 2003 08:00 |
|
Electric Sheep One
Member # 3431
|
written Thursday, November 15 2007 03:57
Profile
For bonus points, generalize to a non-spherical surface. For maximum bonus, do not assume rotational symmetry about the vertical axis. For the heck of it, find the surface that you are always about to leave but never quite do. For alternative heck, find the surface that launches you the farthest horizontal distance from the point at which you leave it, without ever taking you below ground level, and (of course) for fixed initial height. [ Thursday, November 15, 2007 04:01: Message edited by: Student of Trinity ] -------------------- We're not doing cool. We're doing pretty. Posts: 3335 | Registered: Thursday, September 4 2003 07:00 |
|
Shock Trooper
Member # 2123
|
written Thursday, November 15 2007 09:10
Profile
quote:Wow, I am not looking forward to my physics class next semester now. >.< -------------------- Rahhar... Posts: 228 | Registered: Monday, October 21 2002 07:00 |
|
Off With Their Heads
Member # 4045
|
written Thursday, November 15 2007 12:38
Profile
Homepage
quote:Augh, that reminds me far too much of my current advanced mechanics course (which is not fun). -------------------- Arancaytar: Every time you ask people to compare TM and Kel, you endanger the poor, fluffy kittens. Smoo: Get ready to face the walls! Ephesos: In conclusion, yarr. Kelandon's Pink and Pretty Page!!: the authorized location for all things by me The Archive of all released BoE scenarios ever Posts: 7968 | Registered: Saturday, February 28 2004 08:00 |
|
Electric Sheep One
Member # 3431
|
written Thursday, November 15 2007 13:34
Profile
When I first posed this particular problem, I too thought it would be some sort of variational monstrosity. But it's amusingly trivial. -------------------- We're not doing cool. We're doing pretty. Posts: 3335 | Registered: Thursday, September 4 2003 07:00 |
|
Off With Their Heads
Member # 4045
|
written Thursday, November 15 2007 14:18
Profile
Homepage
Uh, come to think of it, isn't it just straight down? -------------------- Arancaytar: Every time you ask people to compare TM and Kel, you endanger the poor, fluffy kittens. Smoo: Get ready to face the walls! Ephesos: In conclusion, yarr. Kelandon's Pink and Pretty Page!!: the authorized location for all things by me The Archive of all released BoE scenarios ever Posts: 7968 | Registered: Saturday, February 28 2004 08:00 |
|
Electric Sheep One
Member # 3431
|
written Thursday, November 15 2007 14:23
Profile
For some reason I was thinking that the problem also stipulated an initial velocity. But yes, in general you just find the free trajectory under gravity, so a parabola, and tack your roof to it. -------------------- We're not doing cool. We're doing pretty. Posts: 3335 | Registered: Thursday, September 4 2003 07:00 |
|
Off With Their Heads
Member # 4045
|
written Thursday, November 15 2007 14:47
Profile
Homepage
I bet it would be more fun in a Lagrangian formulation. :P -------------------- Arancaytar: Every time you ask people to compare TM and Kel, you endanger the poor, fluffy kittens. Smoo: Get ready to face the walls! Ephesos: In conclusion, yarr. Kelandon's Pink and Pretty Page!!: the authorized location for all things by me The Archive of all released BoE scenarios ever Posts: 7968 | Registered: Saturday, February 28 2004 08:00 |
|
Infiltrator
Member # 4256
|
written Thursday, November 15 2007 17:25
Profile
I doubt that problem would be helped by the of Lagrangian in any way shape or form. Maybe if the brick was also attached to a compressed spring that was pushing it towards the igloo... Have you gotten to putting extra conditions into your motion yet? That problem was from an intro physics course, that I still like to pull random questions from to review, it helped quite a bit on the pGRE. Another problem from there that I can't remember how to solve, is at what height on a q-ball should a horizontal force be applied to the ball doesn't skid (on a surface with set friction coefficients). Actually, I'm probably not even remembering the question correctly, but it was something like that. Also, the 'furthest' launch would just be any object with a 'flat' edge somewhere along the shape. How far that edge has to be off the ground would probably depend on the objects initial velocity, but no other factor would matter. -------------------- "Let's just say that if complete and utter chaos was lightning, he'd be the sort to stand on a hilltop in a thunderstorm wearing wet copper armour and shouting 'All gods are false'." Posts: 564 | Registered: Wednesday, April 14 2004 07:00 |
|
Electric Sheep One
Member # 3431
|
written Thursday, November 15 2007 20:09
Profile
quote:Right. -------------------- We're not doing cool. We're doing pretty. Posts: 3335 | Registered: Thursday, September 4 2003 07:00 |
|
Master
Member # 4614
|
written Monday, November 26 2007 15:21
Profile
Homepage
Back comes this topic. :cool: The two blocks shown are released from rest. If the coefficient of kinetic friction between the blocks and the surfaces on which they slide is 0.20, what is the magnitude of the acceleration of either block? Blocks: 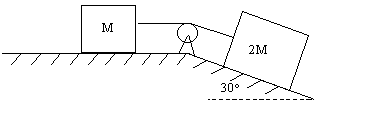 So, for the block on the slope: T = 2(umg cos(30) + mg sin(30) + ma) based on the last problem we did. For the block on the horizontal surface, ma = T - f T = ma + f 2(umg cos(30) + mg sin(30) + ma) = ma + umg ma = 2(umg cos(30) + mg sin(30) + ma) - umg Cancel out the mass and get the a's on one side: a = -(2ug cos(30) + 2g sin(30) - ug) Doing the calculations gives me -11.24 m/s^2, not one of my options. What did I do wrong here? Once again, thanks for your help. -------------------- -ben4808 Posts: 3360 | Registered: Friday, June 25 2004 07:00 |
|
...b10010b...
Member # 869
|
written Monday, November 26 2007 15:23
Profile
Homepage
You can't just cancel out the mass like that when there's addition on one side of the equation. -------------------- The Empire Always Loses: This Time For Sure! Posts: 9973 | Registered: Saturday, March 30 2002 08:00 |
|
By Committee
Member # 4233
|
written Monday, November 26 2007 16:03
Profile
Dude, you aren't cheatin', are you? 'Cause that ain't cool. -------------------- In today’s America, there are more World of Warcraft players than farmers. Posts: 2242 | Registered: Saturday, April 10 2004 07:00 |
Pages
- 1
- 2
